De l’objet au figuré : l’abstraction en cartographie
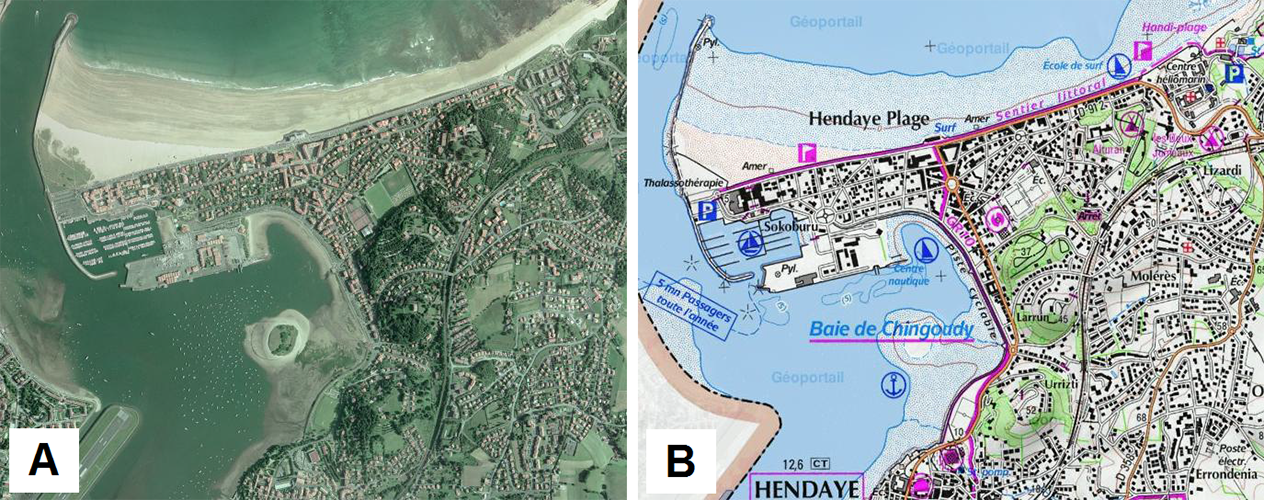
Représenter un espace géographique sur une carte topographique, c’est avant tout simplifier l’information qui le caractérise pour faciliter sa compréhension. Ce processus de simplification est appelé abstraction. Il consiste à transformer une représentation réaliste en une autre plus abstraite en conservant uniquement l’information la plus significative. En réduisant ainsi la quantité d’informations, l’abstraction rend l’information plus assimilable et compréhensible pour les utilisateurs. La figure 1 illustre les différences visuelles entre une représentation cartographique réaliste : une orthophotographie (A) et une abstraction cartographique : la carte topographique IGN au 1:25 000e (B). Grâce à sa forme simplifiée, la carte topographique permet aux utilisateurs d’accéder plus facilement et plus rapidement aux différentes informations géographiques représentées.
Figure 1 : Différences entre un rendu photoréaliste : l’orthophotographie (A) et une abstraction cartographique : la carte topographique IGN au 1:25 000ème (B)
Source : Hoarau, 2015. |
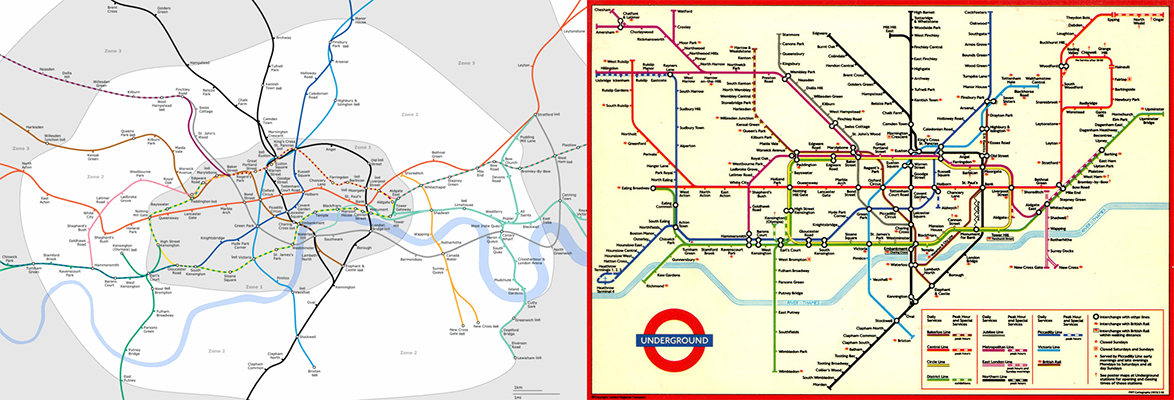
La quantité d’informations représentées définit le niveau d’abstraction. Plus l’information est simplifiée, plus le niveau d’abstraction augmente. La figure 2 illustre deux représentations cartographiques possédant un haut niveau d’abstraction, les cartes de métro. Sur ces deux cartes du métro londonien, seules les lignes et les stations de métro sont représentées de manière schématique. Cette simplification de l’information rend la carte facilement interprétable et compréhensible pour les utilisateurs.
Figure 2 : Deux cartes schématiques du métro londonien
Sources : à gauche, London Underground geographic maps project, logiciel écrit par ed g2s et James D. Forrester à partir de données GPS data, sur Wikimedia Commons (CC BY-SA 3.0). À droite, carte photographiée par Roger W, 1994, FlickR (CC BY-SA 2.0) |
McCloud (1993) rappelle qu’il existe deux types de simplification :
1. La simplification du niveau de détail : il s’agit d’une simplification du sens par élimination des détails pour ne conserver que les plus significatifs. Par exemple, sur la figure 1, pour représenter le territoire, seuls les éléments topographiques significatifs sont conservés, les routes, le bâti, etc.
2. La simplification des propriétés visuelles (la forme, la couleur, etc.) : les propriétés visuelles des éléments topographiques sont simplifiées pour accentuer leur perception. Par exemple, sur la figure 1, la forme des routes sont simplifiés pour accentuer leur courbure ou leur linéarité.
Cette simplification de l’information passe par la construction de signes graphiques. Dans un premier temps, nous exposons les connaissances relatives aux principes de fonctionnement des signes graphiques. Dans un deuxième temps, nous détaillons les différents processus d’abstraction en jeu dans la construction des signes graphiques d’une carte topographique.
1. Les signes graphiques : donner du sens à l’information géographique
|
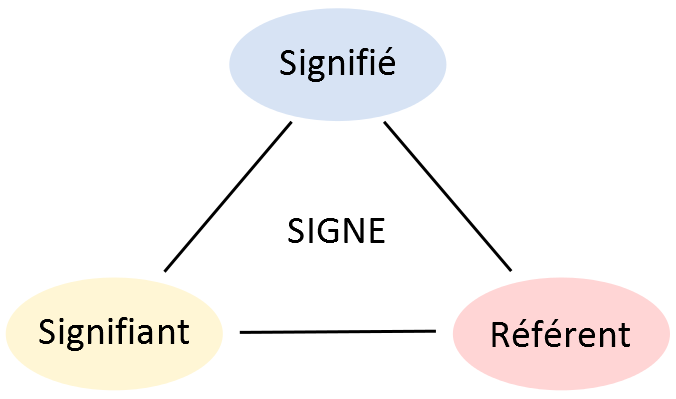
Pour communiquer entre eux, les hommes utilisent différents langages qui s’appuient sur des systèmes de signes (Saussure, 1915 ; Shannon et Weaver, 1949 ; Pierce, 1978 ; Eco, 1988). Le signe est le substitut d’un objet ou d’une chose, qui désigne à la fois ce qu’un individu perçoit et l’image mentale associée à cette perception. Par exemple, le mot « télévision » est un substitut de l’objet « télévision », permettant d’énoncer et de faire référence à celle-ci dans une communication entre individus, qu’elle soit orale ou écrite : « je regarde la télévision ». Les signes possèdent une structure à trois faces formant un triangle sémiotique illustré par la figure 3 : le référent (ce dont on parle), le signifiant (la forme du signe, par exemple un mot), le signifié (le sens, c’est-à-dire le contenu du signe). La sémiologie est la science qui étudie les propriétés des signes et les rapports qu’ils entretiennent avec l’information qu’ils expriment (Saussure, 1915). Nous nous intéressons ici à une branche de la sémiologie appelée sémiologie graphique. Elle propose notamment un ensemble de règles de construction des signes graphiques dont l’objectif est de faciliter la transmission d’une information. Le langage cartographique s’appuie sur la construction de signes graphiques. |
Figure 3 : Le triptyque référent-signifiant-signifié représentant le concept de signe.
Source : Ory, 2017 |
1.1. Les principes de fonctionnement des signes graphiques
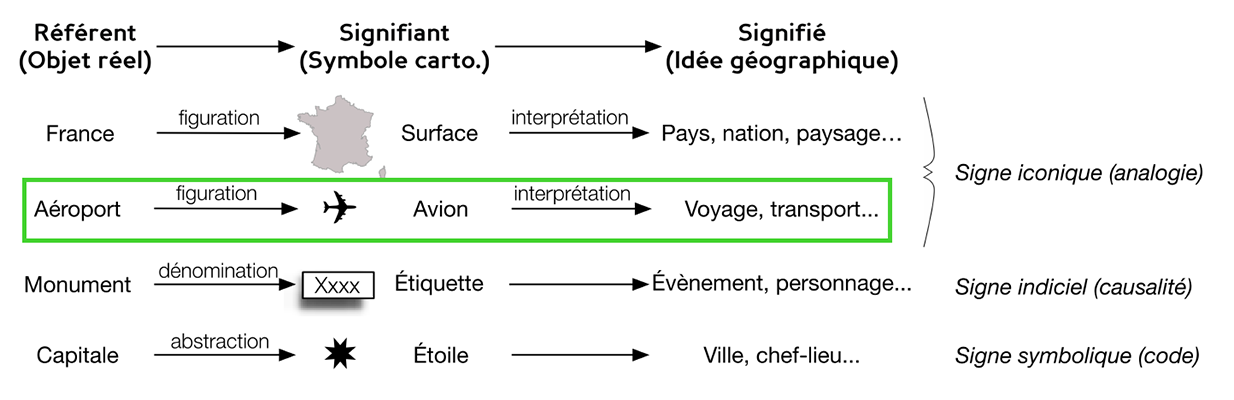
La figure 4 ci-dessous présente le fonctionnement des signes graphiques en cartographie au travers du triptyque : référent-signifiant-signifié.
Figure 4 : Fonctionnement des signes graphiques en cartographie
Source : Ory, 2016 d'après Jégou, 2013. |
Le référent constitue l’objet réel ou le concept qui doit être interprété par l’utilisateur au travers du signe. Il existe une distinction nette entre le signe et le référent. Dans son tableau La trahison des images, René Magritte ajoute la légende « Ceci n’est pas une pipe ». Magritte matérialise ainsi la différence entre le signe et son référent, même représentée de manière très réaliste, une pipe peinte dans un tableau n’est pas une vraie pipe que l’on peut fumer. En cartographie, le référent constitue un objet réel de l’espace géographique qui devra être interprété par l’utilisateur en lisant la carte. Il peut s’agir d’un espace géographique dans sa globalité, par exemple la France, d’un objet physique, par exemple un aéroport ou un monument, ou bien d’un concept, par exemple une capitale.
Le signifiant est la matérialisation visuelle du signe graphique, c’est-à-dire le symbole cartographique utilisé pour représenter le référent. Le signifiant joue le rôle de médiateur entre le référent et le signifié. Il aide l’utilisateur à rentrer en contact avec le signe, à travers une représentation du référent. Le signifiant peut prendre différentes formes telles qu’un mot, un pictogramme, un dessin simplifié, etc. Selon Pierce (1978), le signifiant peut avoir trois formes différentes :
1. L’icône renvoie à un objet signifié grâce à sa ressemblance. Le signifiant a ainsi une relation de similarité avec son référent. Les dessins figuratifs utilisés en bande dessinée peuvent être considérés comme des icônes. Autre exemple, le pictogramme « avion » de l’encadré vert de la figure 4, est interprété comme un aéroport par les utilisateurs à cause des similarités et des ressemblances existantes entre le signe et la réalité.
2. L’indice est un signe qui exprime quelque chose de différent de ce qu’il représente réellement. Le signifiant a ainsi une relation causale. Par exemple, un nuage noir sur une carte météorologique indique un risque de pluie.
3. Le symbole rompt avec toute ressemblance avec l’objet ou la chose exprimée. Les symboles renvoient à l’objet au moyen d’une convention d’ordre culturel qui repose sur une association d’idées ou de valeurs. Par exemple, la colombe représente la paix pour l’ensemble de la communauté internationale. Cette interprétation n’est pas en lien avec la fonction naturelle de la colombe, il s’agit là d’une acceptation collective. De la même manière, en France, les routes sont régulièrement représentées par des symboles linéaires de couleurs vives (IGN, Michelin), or dans la réalité, les routes ne sont pas bleues, rouges ou oranges.
Le signifié désigne la représentation mentale de l’objet ou du concept auquel le signe est rattaché. Lorsqu’un utilisateur lit ou entend le mot « moto », il s’en fait une représentation mentale. Celle du type de moto qu’il connaît le mieux : deux roues, un guidon, une selle, etc. En cartographie, Jégou (2013) souligne que le signifié constitue une idée géographique. Sur le deuxième exemple de la figure 4, le pictogramme représentant un avion (le signifiant) apporte une idée de voyage et de transport (le signifié).
La difficulté dans la construction d’une carte réside dans le choix des signes graphiques afin de délivrer un message visuel explicite et permettant une compréhension aisée de l’espace géographique représenté.
1.2. Les règles de construction des signes graphiques
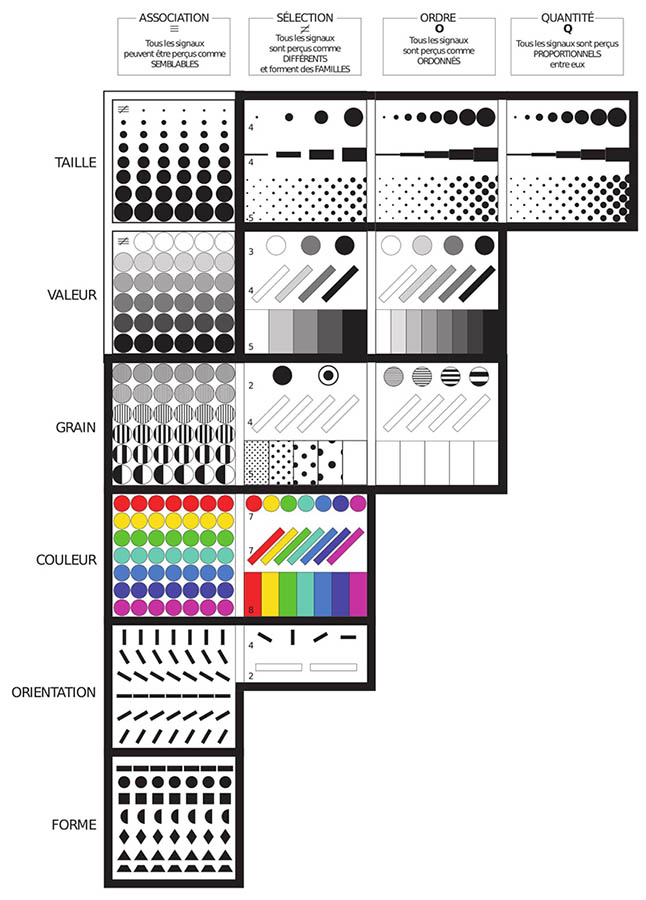
Au même titre que l’expression verbale, l’expression graphique a ses exigences qui impliquent la mise en œuvre de règles de conception (Chombart de Lauwe et al., 1952). Jacques Bertin, père de la sémiologie graphique, travailla à la rédaction d’une grammaire graphique basée sur l’utilisation et la manipulation de variables visuelles garantissant une transmission correcte du message cartographique entre la carte et son utilisateur. La figure 5 illustre les différentes variables visuelles constituant cette grammaire graphique :
1. La taille correspond à la variation de la surface des symboles représentés ;
2. La valeur correspond au rapport entre les quantités de noir et de blanc dans les couleurs des symboles représentés ;
3. Le grain correspond à la quantité de tâches que l’on peut percevoir sur une surface uniforme ;
4. La couleur correspond à la sensation physiologique résultant des radiations reçues par l’œil en regardant un objet éclairé par une lumière blanche (lumière solaire) ;
5. L’orientation correspond à l’angle des symboles représentés avec l’horizontale ;
6. La forme correspond à la structure externe des symboles ponctuels et linéaires et à la structure interne des symboles surfaciques.
|
L’intérêt de ces variables visuelles réside dans leurs échelles de perception différentes, que Bertin appelle « longueur ». Il s’agit du nombre de variations différenciables et perceptibles par l’œil humain qu’offre la variable visuelle. Par exemple, la variable visuelle « taille » offre une possibilité de variation assez grande comme l’illustre la figure 5 avec les variations de taille des différents symboles. On dira alors que son échelle de perception est longue. L’échelle de perception des variables visuelles permet de transcrire différents types de relations visuelles entre les différents signes graphiques d’une composition cartographique. Elles sont dites : 1. associatives, si elles permettent de percevoir plusieurs signes graphiques de manière groupée grâce à leur ressemblance ou leur similarité. Par exemple, à la lecture d’une carte thématique, un utilisateur doit être en capacité d’identifier rapidement tous les signes graphiques de forme ronde, quelle que soit leur couleur ou leur position. 2. sélectives, si elles permettent de différencier et d’identifier instantanément un signe graphique ou un groupe de signes graphiques du reste de la composition. Par exemple, à la lecture d’une carte thématique, un utilisateur doit être en capacité d’identifier rapidement tous les signes graphiques rouges, quelle que soit leur forme ou leur position. 3. ordinales, si elles permettent de percevoir de manière spontanée l’ordre entre les différents signes graphiques de la carte, c’est-à-dire de les classer entre eux selon leur valeur. Par exemple, à la lecture d’une carte thématique, un utilisateur doit être en capacité d’identifier rapidement si le cercle représentant la population d’une ville est plus petit ou plus grand que la ville voisine. 4. quantitatives, si elles permettent de percevoir les proportions relatives entre les différents signes graphiques de la carte. Il s’agit de la distance visuelle, qui permet d’évaluer la quantité qui différencie deux signes graphiques. Par exemple, à la lecture d’une carte thématique, un utilisateur doit être en capacité d’identifier rapidement le ratio de population entre deux villes représentées par des cercles proportionnels. Le tableau de la figure 5 synthétise les règles sémiologiques proposées par Bertin. Elles constituent des recommandations pour la construction de représentations graphiques, en spécifiant la concordance entre l’utilisation d’une variable visuelle et les relations visuelles recherchées par le cartographe. Par exemple, si le cartographe cherche à montrer une relation quantitative, il devra utiliser la variable visuelle « taille ». La prise en compte de ces règles sémiologiques dans les processus de conception cartographique permet d’assurer que l’information est interprétable par les utilisateurs. |
Figure 5 : Le tableau de concordance des variables visuelles et des relations graphiques (Bertin, 1973)
Source : Réalisation de Laurent Jégou, d'après Bertin, 1973. |
2. Les processus d’abstraction cartographique pour les cartes topographiques
|
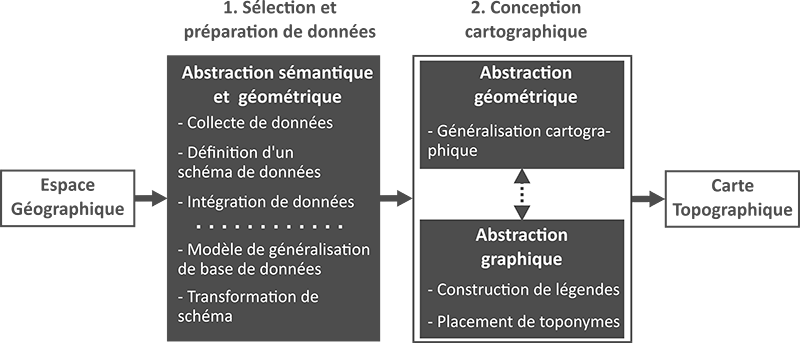
L’objectif d’un producteur de cartes est d’assurer que tous les éléments visuels contenus dans la carte soient facilement perçus et correctement interprétés par l’utilisateur. La figure 6 illustre les principales étapes de modélisation spatiale nécessaires à la construction d’une carte topographique : (1) la sélection et la préparation de données et (2) la conception cartographique. Chacune de ces étapes fait intervenir des processus d’abstraction cartographique de natures différentes : l’abstraction sémantique, l’abstraction géométrique et l’abstraction graphique (Hoarau, 2015). L’abstraction sémantique vise à réduire la complexité sémantique de l’information géographique en sélectionnant les données correspondant à un usage donné. L’abstraction géométrique a pour objectif de simplifier le niveau de détail géométrique des données géographiques sélectionnées afin de permettre leur perception à une échelle donnée. L’abstraction graphique constitue l’étape de symbolisation des données à travers la construction de légende. Ensemble, les trois processus d’abstraction permettent de retranscrire une réalité géographique sur une carte à échelle réduite. Ils mettent en forme l’information géographique qui composera la future carte topographique. |
Figure 6 : Étapes de construction d’une carte topographique et les processus d’abstraction cartographique associés
Source : Ory, 2016, figure adaptée de Duchêne et al., 2011. |
2.1. L’abstraction sémantique : la sélection de données
À travers la formule : « la carte n’est pas le territoire », Korzybski (1998) précise qu’une carte n’est pas exhaustive et qu’elle constitue une vue sélective de l’espace géographique représenté. L’abstraction sémantique constitue cette sélection, qui consiste à adapter le contenu cartographique aux usages de la carte. Il s’agit d’effectuer une analyse des usages de la future carte et de déterminer ainsi les différents éléments géographiques qui devront être représentés. L’abstraction sémantique constitue donc une réduction quantitative de l’information géographique en déterminant les objets géographiques retenus pour modéliser le monde réel en adéquation avec un usage donné. Par exemple, pour une carte topographique, il s’agit de conserver le bâti, le réseau routier, les limites administratives, le réseau hydrographique et divers éléments topographiques. Ainsi, des différences subsisteront toujours entre une carte, c’est-à-dire les données géographiques retenues et l’espace géographique référent.
2.2. L’abstraction géométrique : la généralisation
L’abstraction géométrique, également appelée généralisation, permet d’adapter le niveau de détail géométrique des données géographiques à l’échelle de perception. Le niveau de détail géométrique correspond à la finesse de la description géométrique de l’objet représenté. La figure 7 illustre trois échelles de représentation du bâti : 1:25 000e, 1:50 000e et 1:100 000e. Sur cet exemple, les données cartographiques de type « bâti » sont dérivées d’une grande échelle, le 1:25 000e vers une échelle plus petite, le 1:100 000e, en subissant des transformations géométriques mises en œuvre par le processus de généralisation cartographique. Ces opérations de transformations géométriques sont indispensables pour adapter le niveau de détail des objets cartographiques et les rendre correctement perceptibles et interprétables par les utilisateurs.
Figure 7 : Exemple de généralisation cartographique sur le bâti
NB : Les échelles sont données à titre démonstratif puisqu'à l'écran, les échelles numériques ne peuvent être conservées. Source : Ory, 2016, figure adaptée de Regnauld, 1998. |
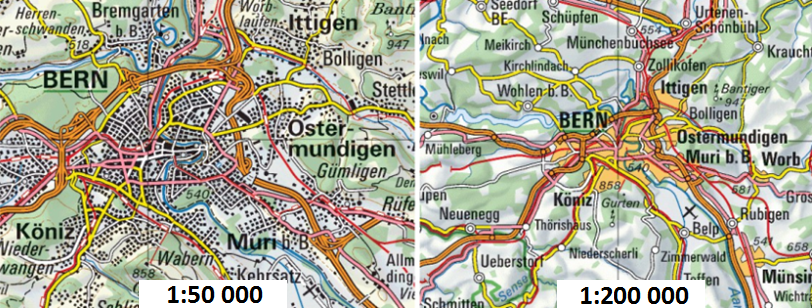
Au 1:100 000e, les objets « bâtiments » ne peuvent plus être perçus par les utilisateurs, s’ils sont trop grossis ; des conflits géométriques apparaissent entre les objets, c’est pourquoi ils sont totalement agrégés, devenant une nouvelle classe d’objets « bloc urbain ». La figure 8 illustre ce principe à travers l’exemple de la carte topographique Swisstopo représentant la ville de Berne à deux échelles de représentation différentes : 1:50 000e et 1:200 000e. Sur cet exemple, au 1:200 000e, le bâti est totalement agrégé pour devenir un bloc urbain.
Figure 8 : Illustration de la généralisation cartographique à travers l’exemple de Swisstopo
Source : Swisstopo |
|
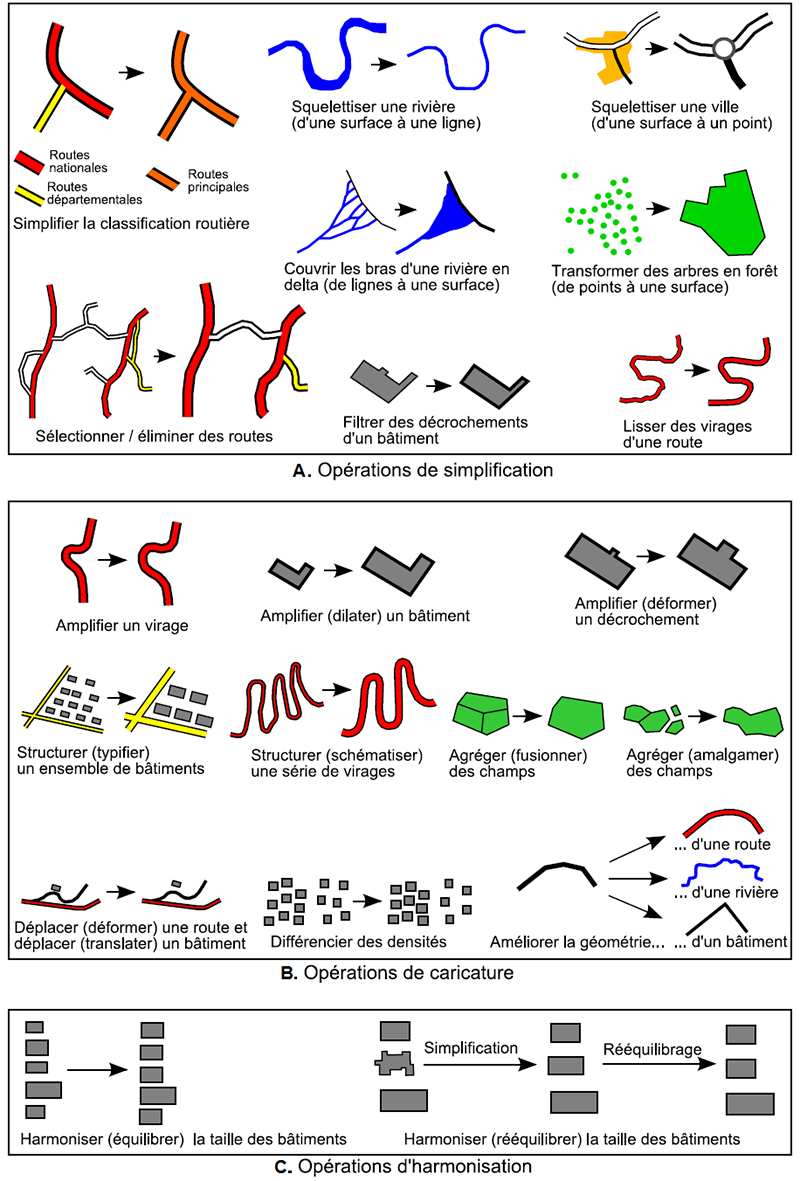
Les opérations de transformation géométrique subies par les objets cartographiques sont de plusieurs natures. La figure 9 illustre la classification proposée par Mustière (2001) : opérations de simplification (partie A), opérations de caricature (partie B) et opérations d’harmonisation (partie C). Les opérations de simplification consistent à simplifier les données cartographiques en éliminant de l’information. La partie A de la figure 9 illustre différents exemples d’opérations de simplification : simplification géométrique du niveau de détail d’un bâtiment ou d’un virage de route, élimination d’informations sur un réseau routier, changement d’implantation pour un bras de cours d’eau et une forêt, etc. Les opérations de caricature consistent à supprimer ou accentuer certains détails caractéristiques des objets cartographiques en fonction de leur degré d’importance dans le message cartographique délivré et faciliter leur perception par les utilisateurs. La partie B de la figure 9 illustre différents exemples d’opérations de caricature : amplifier la courbure d’un virage, amplifier le décrochement d’un bâtiment, fusionner des champs, structurer des bâtiments, etc. Les opérations d’harmonisation ont pour objectif d’effectuer un rééquilibrage géométrique global du niveau de détail, en gommant les différences géométriques peu perceptibles (Mustière, 2001) et en rétablissant les relations spatiales entre les objets cartographiques qui ont été modifiées par les opérations de simplification et de caricature. Par exemple, il peut s’agir de rétablir les distances entre deux objets cartographiques, de rééquilibrer les angles ou l’aire de différents objets cartographiques, etc. La partie C de la figure 9 illustre différents exemples d’opérations d’harmonisation dont l’objectif est de faciliter la compréhension de structures spatiales particulières : un alignement de bâtiments. Les opérations de généralisation sont effectuées sous contraintes afin de conserver la structure et les éléments caractéristiques de la réalité du terrain. Il existe plusieurs types de contraintes : de lisibilité, de forme, sémantiques, spatiales, etc. (Ruas et Plazanet, 1996 ; Weibel et Dutton, 1999). Les opérations sont appliquées itérativement, jusqu’à atteindre une satisfaction maximale de ces contraintes. |
Figure 9 : Principales opérations utilisées en généralisation cartographique
Source : Mustière, 2001. |
2.3. L’abstraction graphique : la construction de légende
|
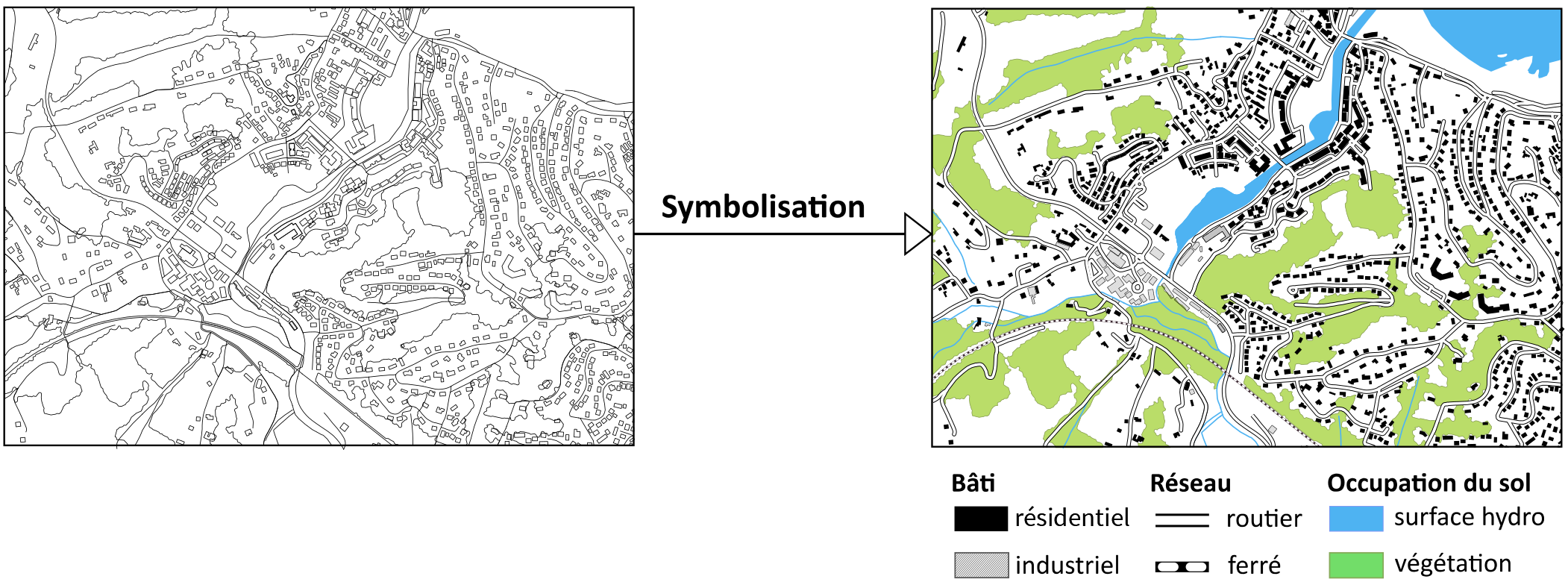
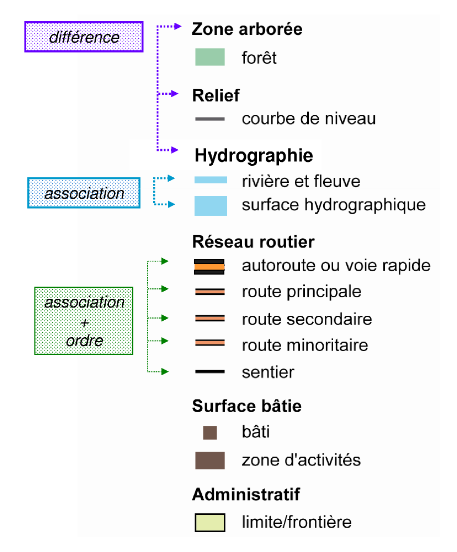
Les données cartographiques sont ensuite organisées visuellement grâce au processus d’abstraction graphique : la construction de légende. Cette étape consiste à choisir les signes graphiques pour l’ensemble des objets cartographiques contenus dans la carte. L’objectif est de construire des relations signes-sens facilement interprétables. La figure 10 illustre les signes graphiques choisis pour quatre thèmes cartographiques différents : zone arborée, relief, hydrographie et réseau routier. Le thème hydrographie comprend deux sous-thèmes « rivière et fleuve » et « surface hydrographique », qui se différencient par leur implantation, linéaire pour le premier, surfacique pour le second. Les signes graphiques choisis font émerger des relations visuelles et sémantiques entre les différents thèmes et sous-thèmes cartographiques. Par exemple, la figure 10 illustre différents types de relations visuelles, telles que la relation associative pour le thème hydrographie à travers l’utilisation de la variable visuelle couleur - le bleu. De même, l’utilisation de la variable visuelle taille permet de délivrer une relation d’ordre sur le réseau routier. Le processus de construction de légende est un processus créatif, où le cartographe fait intervenir ses goûts et ses préférences (Christophe, 2011). Les signes graphiques choisis en légende sont appliqués automatiquement sur un jeu de données cartographiques, il s’agit du processus de symbolisation. La figure 11 illustre le processus de symbolisation pour trois thèmes cartographiques : bâti, réseau et occupation du sol. Figure 11 : Processus de symbolisation d’un jeu de données cartographiques
Source : figure adaptée de Ory, 2016 |
Figure 10 : Exemple de relations visuelles et sémantiques entre des thèmes cartographiques
Source : Chesneau, 2006. |
Conclusion
Grâce au système de codage visuel sur lequel s’appuient les cartes topographiques, les divers éléments naturels et artificiels visibles à la surface du sol (la végétation, l’hydrographie, la bâti, les réseaux de communication, etc.) peuvent être représentés conjointement. Interpréter une carte topographique n’est pas une activité facile surtout si l’utilisateur n’est pas familier des principes d’abstraction utilisés par le concepteur de cartes. La légende constitue la clé de lecture et de compréhension, elle permet d’identifier facilement la nature des objets géographiques représentés et les relations qu’entretiennent les objets entre eux. Changer ses habitudes cartographiques en lisant une carte conçue par un producteur de cartes non connu nécessite le plus souvent de réapprendre les principes d’abstraction utilisés. En effet, chaque producteur représente l’espace géographique à sa façon avec des pratiques cartographiques propres qui définissent son « style ».
Pour compléter
- Un manuel : TIFFOU J., Commenter la carte topographique aux examens et concours, Armand Colin, coll. U, 2009 (réed.). Site de l'éditeur.
- Un article : PALSKY, G., 2017, « La Sémiologie graphique de Jacques Bertin a cinquante ans ! », VisionsCarto, juin 2017.
Bibliographie de référence
- BERTIN, J. (1973). Sémiologie graphique, Les diagrammes - Les réseaux - Les cartes, 2e édition, (1ère édition : 1967). Mouton Gauthier-Villar, Paris.
- CHESNEAU, E. (2006). Modèle d’amélioration automatique des contrastes de couleur en cartographie : Application aux cartes de risque. Thèse de doctorat en Sciences de l’Information Géographique, Université Paris-Est, IGN / COGIT.
- CHOMBART DE LAUWE, P. H., ANTOINE, S., BERTIN, J., CHAUVET, L., COUVREUR, L., et GAUTHIER, J. (1952). Paris et l’agglomération parisienne, Tome I : « L’espace social dans une grande cité ». Puf, Coll. Bibliothèque de Sociologie Contemporaine.
- CHRISTOPHE, S. (2011). "Creative Colours Specification Based on Knowledge" (COLorLEGend system). The Cartographic Journal, 48(2), p. 138-145.
- DUCHÊNE, C., CHRISTOPHE, S., et RUAS, A. (2011). "Generalisation, symbol specification and map evaluation: feedback from research done at COGIT laboratory, IGN France". Special Issue : Validation of EO-derived information for crisis management: a Digital Earth perspective in the VALgEO expert community. International Journal of Digital Earth (IJDE), 4(1), p. 25-41.
- ECO, U. (1988). Le signe. Éditions Labor, Bruxelles.
- JÉGOU, L. (2013). Vers une nouvelle prise en compte de l’esthétique dans la composition de la carte thématique : propositions de méthodes et d’outils, Thèse de doctorat en Géographie. Université Toulouse le Mirail - Toulouse II.
- KORZYBSKI, A. (1998). Une carte n’est pas le territoire: prolégomènes aux systèmes non-aristotéliciens et à la sémantique générale, Éditions de l’Éclat, Paris, France. (présentation de l'éditeur)
- HOARAU, C. (2015). Représentations cartographiques intermédiaires : Comment visualiser une carte et une orthophotographie pour naviguer entre abstraction et réalisme ?, Thèse de doctorat en Sciences et Technologies de l’Information Géographique. Université Paris-Est, IGN / COGIT.
- MCCLOUD, S. (1993). Understanding comics: The invisible art. William Morrow Paperbacks, New York. (voir la Notice Wikipédia)
- MUSTIÈRE, S. (2001). Apprentissage supervisé pour la généralisation cartographique, Thèse de doctorat en Informatique - Intelligence Artificielle. Université Paris VI.
- ORY, J. (2016). Connaissances pour la perception et la construction de styles topographiques, Thèse de doctorat en Sciences et Technologies de l’Information Géographique. Université Paris-Est, IGN / COGIT.
- PIERCE, C. S. (1978). Écrits sur le signe. Le Seuil, Paris. Compte-rendu d'Ugomaria Olivieri dans la Revue philosophique de Louvain.
- REGNAULD, N. (1998). Généralisation du bâti : Structure spatiale de type graphe et représentation cartographique. Thèse de doctorat en Informatique. Université de Provence, IGN / COGIT. (pdf)
- RUAS, A., et PLAZANET, C. (1996). "Strategies for automated map generalisation". In : Proceedings of the 7th International Symposium on Spatial Data Handling (SDH’96), 12-16 August 1996, Delft, Netherlands. (pdf)
- SAUSSURE, F. (1915). Cours de linguistique générale. Lausanne et Paris : Payot. (Notice dans l'Encyclopædia Universalis)
- SHANNON, C. E., et WEAVER, W. (1949). The mathematical theory of information. 1st Edition, University of Illinois Press, Urbana.
- WEIBEL, R., et DUTTON, G. (1999). "Generalising spatial data and dealing with multiple representations". In : P. Longley, M.F. Goodchild, D.J. Maguire and D.W.Rhind (Eds.), Geographical Information Systems : Principles, Techniques, Management and Applications, , 2nd Edition, Cambridge, GeoInformation International, p. 125-155. (pdf)
Sites utiles
- Geoportail.gouv.fr
- Education.ign.fr
- Petit historique des cartes de France IGN géantes (1990-2012), Planète Terre sur France Culture, janvier 2012.
- Dessiner le monde (1/4) : De l’instabilité de la carte, CulturesMonde sur France Culture, décembre 2012.
- Des cartes à notre image, Tout un monde sur France Culture, mars 2017.
- Espace interministériel de l’information géographique : Glossaire de l’information géographique
- Ressources naturelles Canada
- Généralisation cartographique dans Wikipédia
- Définition de Topographie dans HyperGeo
- Association Française de Topographique : Lexique topographique
Jérémie ORY,
post-doctorant en géovisualisation, Laboratoire en sciences et technologies de l’information géographique (LaSTIG), équipe COGIT, IGN France
Mise en web : Jean-Benoît Bouron
Pour citer cet article :
Jérémie Ory, « De l’objet au figuré : l’abstraction en cartographie », Géoconfluences, 2017. |
Pour citer cet article :
Jérémie Ory, « De l’objet au figuré : l’abstraction en cartographie », Géoconfluences, septembre 2017.
http://geoconfluences.ens-lyon.fr/informations-scientifiques/articles/objet-figure-cartographie


 Mode zen
Mode zen