Savoir faire


  Mesures, normes et transports

 Étude d'un réseau : initiation à l'analyse topologique et à l'étude des graphes. Des applications

 Recherche et suivi d'itinéraires, suivi de déplacements

 Mesures, normes et transports

Il peut être utile de faire le point sur les unités de mesure le plus souvent employées dans le monde des déplacements et du transport.

Les capacités de charge

La capacité de charge d'un moyen de transport est le poids maximal autorisé qu'il est habilité à transporter.
Pour les navires, c'est la capacité cubique intérieure ou la capacité de transport. On parle de jauge ou de tonnage, elle est exprimée en tonneaux. 1 tonneau équivaut à 100 pieds cube ou 2,83 m3.
La capacité peut être totale : la jauge brute ou tonnage brut (tonneaux de jauge brute ou tjb) désigne le volume des espaces fermés du navire à l'exception du double fond. La capacité peut être "utile", c'est la jauge nette (tjn) ou tonnage net qui désigne le volume de la capacité commerciale du navire.
On évoque aussi le déplacement d'un navire qui est le volume d'eau déplacé par sa carène, rigoureusement égal à sa masse totale. On distinguera le déplacement en charge du déplacement lège. Le port en lourd (tonnes de port en lourd, tpl) désigne la capacité de chargement d'un navire, le poids maximum qu'il peut transporter, incluant équipage, soutes, vivres, etc.

Pour un véhicule, un avion, la capacité autorisée désigne le nombre maximum de passagers, ou le poids du fret, autorisés à bord compte tenu de la réglementation.

Les mesures de la conteneurisation

L'unité de base employée couramment est l' "Equivalent vingt pieds" (EVP ou Twenty feet equivalent unit, TEU) qui est une mesure nominale de capacité des navires porte-conteneurs, calculée en nombre de conteneurs de 20 pieds pour la longueur, 8,6 pieds pour la hauteur, 8 pieds pour la largeur. Cette norme correspond à la taille la plus courante des conteneurs. Mais il existe également des 45 pieds. Et, de plus en plus, la capacité d'un porte-conteneur s'évalue en terme de cellules (ou slots) offertes.
La nécessité de passer le canal de Panama impose des normes aux navires porte-conteneurs. Ils ne peuvent alors dépasser 70 000 tpl (tonnes de port en lourd), 32,30 m de large, 274,50 m de long, 12 m de tirant d'eau. Les navires plus grands (les porte-conteneurs de 8 000 EVP ont un tirant d'eau de 15 m) sont dits Overpanamax ou Post-panamax. Récemment des navires de 12 000 EVP ont été mis en service (Suezmax) et les New Post Panamax (NPP) ont une capacité de 15 000 EVP

La mesure des flux

Pour mesurer les flux, il faut tenir compte de la quantité transportée et de la distance franchie : passagers/km ou tonnes/km. Lorsque l'on rapporte cette quantité à une unité de temps on obtient un débit : megabits/seconde ou bauds/seconde pour les télécommunications informatiques, Unité Véhicule Particulier (UVP)/heure pour le trafic routier, etc. Le "Passager - kilomètre transporté" (pkt) est une unité de mesure correspondant au transport d'un passager sur une distance d'1 km.
Le nombre de km/avion est la distance moyenne annuelle parcourue par un aéronef. Il permet de mesurer l'efficacité d'une flotte aérienne : il devrait avoir doublé, en moyenne, sur la période 1995 - 2005. Le kilomètre passager réalisé (kpr) est une unité utilisée aussi en transport aérien pour mesurer le trafic passager réalisé.
Dans le transport aérien toujours, le Work Load Unit (WLU) est une unité qui correspond à un passager ou 0,1 tonne de fret, ce qui permet de quantifier l’ensemble du trafic.

  Étude d'un réseau : initiation à l'analyse topologique et à l'étude des graphes

L'étude des réseaux de transport peut être prolongée par la prise en compte des connaissances mathématiques sur les graphes. Elle est particulièrement propice à des travaux en partenariat avec les enseignants de mathématiques (classes de terminale "sciences économiques et sociales"), voir :
www.eduscol.education.fr/index.php?./D0015/Intentions.htm

Pour connaître objectivement et analyser la structure d'un réseau (sa topologie), il doit être représenté sous forme de graphe. On fait remonter la théorie des graphes au problème dit "des ponts de Königsberg" résolu par Leonhard Euler en 1736. Il s'énonçait ainsi : est-il possible, en partant d'une zone de la ville, de retourner dans la même zone en traversant chacun de ses sept ponts une fois et une seule ? En 1822, le mot "graphe" est introduit par l'anglais J.J. Sylvester et, en 1936, paraît un premier livre sur la théorie des graphes écrit par D. König.

De nos jours, la théorie des graphes sert à représenter et à organiser spatialement des tâches (transports, tournées de livraison, par exemple mais tous les modes de communication peuvent être concernés) de manière optimale.

Un graphe est un ensemble de points (nœuds ou sommets ) reliés ou non entre eux par des liens orientés (flèches pour un graphe dit orienté) ou non orientés (arêtes ou arcs). Les nœuds sont à l'origine d'une ou plusieurs lignes (confluence, bifurcation, carrefour). L'étude du graphe d'un réseau permet d'en déterminer les caractéristiques topologiques à partir de paramètres tels que le nombre de nœuds (N), de liens (L) et le nombre de ses composantes connexes (C).

Un graphe est dit complet lorsque deux sommets quelconques et distincts sont reliés par une et une seule arête. Il est dit connexe si l'on peut relier deux sommets quelconques du graphe par une suite continue d'arêtes : ainsi, la connexité indique la possibilité de se rendre de chaque point du réseau à tous les autres par une série de liens. Enfin, la connectivité reflète la complexité d'un réseau lorsqu'il offre plusieurs choix pour aller d'un point à un autre.

Les indices de connectivité permettent d'évaluer les possibilités alternatives d'atteindre les divers sommets d'un réseau. Ils facilitent les comparaisons entre les réseaux et donnent une idée du degré d'achèvement d'un réseau ou des possibilités qui demeurent pour l'étoffer.
Plusieurs indices peuvent être proposés parmi lesquels :
- L'indice ß (bêta) = L/N exprime la complexité d'un réseau, qui s'élève avec le nombre de liens pour un nombre donné de nœuds.
- L'indice g (gamma) est une version standardisée de l'indice précédent, avec une valeur comprise entre 0 et 1. Il exprime le rapport entre le nombre de liens observé et le nombre maximal de liens possibles. Dans le cas d'un graphe planaire, le nombre maximal de lien est égal à 3(N-2), ce qui donne la formule suivante : g (gamma) = L/[3(N-2)]
- Le nombre cyclomatique µ = L-N+C. Il est nul pour un territoire desservi par une série de voies de pénétration sans lien entre elles, il est élevé pour un réseau fortement maillé.
- L'indice a (alpha) est une version standardisée de µ, avec une valeur comprise entre 0 et 1. Cet indice exprime le rapport entre le nombre observé de circuits indépendants et sa valeur maximale. Dans le cas d'un graphe planaire, le nombre maximal de circuits est égal à (2N-5), ce qui donne la formule suivante :
a = (L-N+C)/(2N-5)

Plusieurs autres indices prennent en compte la surface du territoire (S), la longueur du réseau (l) et le trafic (T) calculé d'après le tonnage de marchandises ou le nombre de passagers. La densité du réseau est calculée classiquement par la formule l/S ou par le rapport N/S.
L'indice e (eta) = l/L donne la longueur moyenne des liens (par exemple, de diverses lignes d'une compagnie aérienne).
L'indice i (iota) = T/l exprime le nombre moyen d'unités de trafic (voyageurs ou marchandises) transportées par km.

Les indicateurs locaux de position permettent de mesurer la centralité ou l'accessibilité des différents sommets à l'intérieur d'un graphe. Par exemple :
- La centralité de degré (C_D) correspond au nombre de liaisons directes qui partent d'un sommet. Elle correspond en géographie à la notion de carrefour.
- La centralité d'éloignement moyen (C_E) correspond à la distance moyenne entre un sommet et l'ensemble des autres sommets. Le calcul de cette mesure de centralité implique la construction d'une matrice de distances de plus court chemin à l'intérieur du graphe.

D'après :
- Maurice Wolkdwitsch - Géographie des transports : aménagement et environnement - A. Colin - 1992
- François Plassard - Les réseaux de transport et de communication in Encyclopédie de Géographie, Economica - 1992.
- le cours de Claude Grasland - Université Paris VII / UFR GHSS, année 2000-2001 - Analyse spatiale et modélisation des phénomènes géographiques :
www.grasland.cicrp.jussieu.fr/grasland/go303/ch2/doc_ch2.htm
- les pages du département de Géographie de l'Université Laval (Québec, Canada) > Méthodes d'analyse spatiale, analyse de réseaux : www.ggr.ulaval.ca/Cours/ggr-13470/htm/Semaine09.htm
- Pour compléter, en mathématiques, la théorie des graphes (analyse mathématique des réseaux) à travers le programme de classe terminale de la série ES :
www.eduscol.education.fr/index.php?./D0015/Intentions.htm

  Application à l'étude topologique d'exemples concrets de réseaux

L'analyse topologique fondée sur des données objectives permet de comparer les réseaux de divers territoires. Elle permet aussi de comparer des réseaux à diverses périodes de leur évolution et de réaliser des simulations.
Il s'agit ici de prendre des exemples simples pour comprendre les démarches. On pourra prendre l'exemple de réseaux de métros lorsqu'ils ne sont pas trop complexes. On peut aussi utiliser les réseaux de tramway, les liaisons ferroviaires à grande vitesse, par exemple. Les exemples dépendent de l'échelle des territoires que l'on se propose d'étudier.
Lorsque les réseaux deviennent plus complexes, les traitements de l'information et les calculs doivent être informatisés.

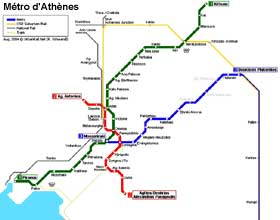
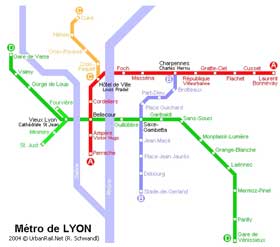
Métros : des exemples de réseaux (Athènes, Lyon, Le Caire et Tunis)

Remarque : les réseaux représentés ci-dessous ne tiennent pas compte de toute l'offre de transport en commun en sites propres (TCSP) des villes concernées qui peut également comporter des lignes de tramways par exemple.

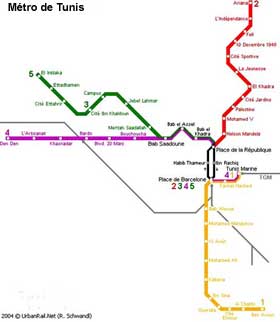Source : UrbanRail.Net - www.urbanrail.net
Avec l'aimable autorisation de Robert Schwandl Verlag - www.robert-schwandl.de

Calculs d'indices de connectivité

	L	N	C	µ L-N+C	ß (Bêta) L/N	g (Gamma) L/[3(N-2)]	a (Alpha) (L-N+C)/(2N-5)
Lyon (sans le réseau de tramway)	13	13	1	1	1	0,39	0,05
Le Caire avant l'extension de réseau	6	6	1	1	1	0,5	0,14
Le Caire après l'extension de réseau	13	10	1	4	1,3	0,54	0,27

Rappel : N = nombre de nœuds ; L = nombre de liens ; C = nombre de ses composantes connexes.

Des données complémentaires (longueurs totales des réseaux, flux, superficies) sont nécessaires pour calculer les indices eta et iota.

Exemples de réseaux en ligne

- les métros du monde : www.urbanrail.net/index.htm
- ou par les "Panoramas des marchés" > Liens utiles du site Interex : www.interex.fr
- ou par www.subwaynavigator.com/subway_site/eng/accueil/fset_subway.htm

Au sujet des mobilités dans les grandes villes d'Égypte, Le Caire plus particulièrement, on pourra consulter différents documents à partir de :
- Conduites urbaines et risques routiers - France - Égypte : http://conduites-urbaines.ens-lsh.fr
- L'observatoire urbain du Caire contemporain (OUCC) : www.cedej.org.eg/rubrique.php3?id_rubrique=35
Accessible à partir de : www.cedej.org.eg

Retour haut de page